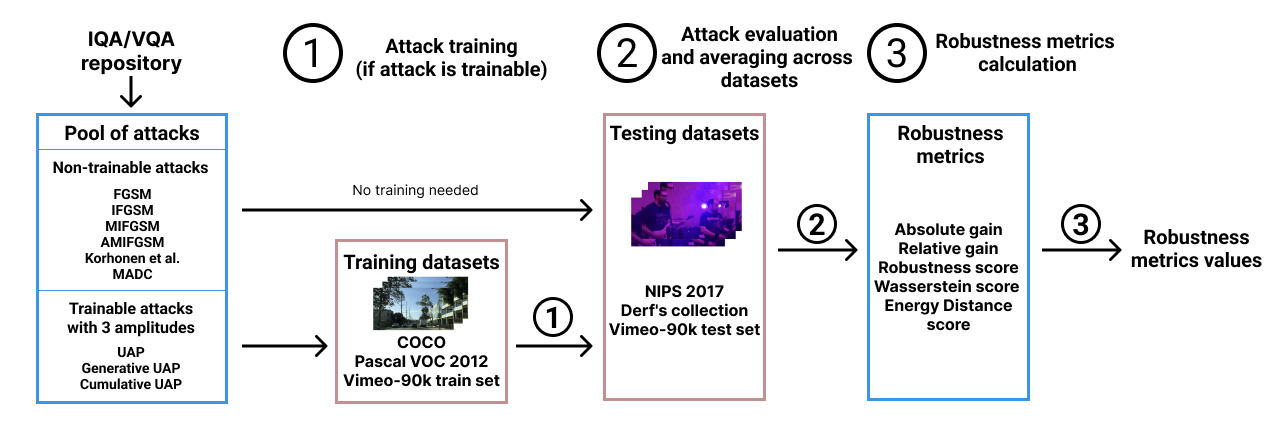
Methodology of the MSU Metrics Robustness Benchmark
Problem definition
Many new image- and video-quality assessment methods (IQA/VQA) are based on neural networks. However, deep-learning-based methods as well as qiality metrics are vulnerable to adversarial attacks. This benchmark aims to investigate metrics’ robustness to perturbation-based and gradient-based adversarial attacks.
Adversarial attacks
For all attacks, the loss function is defined as which increases the attacked IQA/VQA metric score. is computed as the difference between maximum and minimum metric scores calculated on NIPS 2017: Adversarial Learning Development Set[1].
FGSM-based attacks
These attacks are performed specifically on each image. The pixel difference is limited by .
FGSM [2] is a basic approach that makes one gradient step:
$$I^{adv} = I - ε \cdot sign(\nabla_I J(θ, I )).$$
I-FGSM [3] makes gradient steps:
$$I_{t+1}^{adv} = Clip_{I, \varepsilon}\{I_t^{adv} - \alpha \cdot sign(\nabla_I J(\theta, I_t^{adv}))\},$$
where , — input image , — perturbation intensity. The clipped pixel value at position and channel satisfies .
MI-FGSM [4] adds momentum:
$$I_{t+1}^{adv} = Clip_{I, \varepsilon}\{I_t^{adv} - \alpha \cdot sign(g_t)\},t=0,1,\ldots T-1,$$ $$g_t = \nabla_I J(\theta,\ I_t^{adv}) + \nu \cdot g_{t-1},\;\; g_{-1}=0,$$
where controls the momentum preservation.
AMI-FGSM [5]
$$I_{t+1}^{adv} = Clip_{I, 1 / NIQE(I)}\{I_t^{adv} - \alpha \cdot sign(g_t)\},\; t=0,1,\ldots T-1,$$
where , controls the momentum preservation, — score mesured by NIQE [6] quality metric.
Universal Adversarial Perturbation (UAP)-based attacks
Universal adversarial perturbation (UAP) attacks are aimed to generate an adversarial perturbation for a target metric, which is the same for all images and videos. When UAP is generated, the attack process consists of the mere addition of an image with UAP. The resulting image is the image with an increased target metric score. Several ways to generate UAP are listed below.
Cumulative-UAP [7]: UAP is obtained by averaging non-universal perturbation on the training dataset. Non-universal perturbations are generated using one step of gradient descent.
Optimized-UAP [8]: UAP is obtained by training UAP weights using batch training with Adam optimizer and loss function defined as target metric with opposite sign.
Generative-UAP [9]: UAP is obtained by auxiliary U-Net generator training. The network is trained to generate a UAP from random noise with uniform distribution. For training, the Adam optimizer is used, and the loss function is defined as the target metric with the opposite sign. Once the network is trained generated UAP is saved.
Perceptual-aware attacks
Korhonen et al. [10]. This is a method for generating adversarial images for no-reference quality metrics with perturbations located in textured regions. They used gradient descent with additional elementwise multiplication of gradients by a spatial activity map. The spatial activity map of an image is calculated using horizontal and vertical 3×3 Sobel filters.
MADC attack [11] is a method for comparing two image- or video-quality metrics by constructing a pair of examples that maximize or minimize the score of one metric while keeping the other fixed. We choose to keep fixed MSE while maximizing an attacked metric. On each iteration, the projected gradient descent step and binary search are performed. Let be the gradient with direction to increase attacked metric and the gradient of MSE on some iteration. The projected gradient is then calculated as . After projected gradient descent the binary search to guarantee fixed MSE (with 0.04 precision) is performed. The binary search is the process that consists of small steps along the MSE gradient: if the precision is bigger than 0.04, then steps are taken along the direction of reducing MSE and vice versa.
Datasets
| Dataset | Type | Number of samples | Resolution |
|---|---|---|---|
| Training datasets (for UAP attacks) | |||
| COCO [12] | Image | 300,000 | 640 × 480 |
| Pascal VOC 2012 [13] | Image | 11,530 | 500 × 333 |
| Vimeo-90k Train set [14] | Triplets of images | 2,001 | 448 × 256 |
| Test datasets | |||
| NIPS 2017: Adv. Learning Devel. Set [1] | Image | 300,000 | 640 × 480 |
| Derf's collection (blue_sky sequence) [15] | Video | 1 (250 frames) | 1920 × 1080 |
| Vimeo 90k Test set [16] | Triplets of images | 2,001 | 448 × 256 |
Comparison methodology
Robustness scores
Absolute gain
$$Abs. gain = \frac{1}{n}\sum_{i=1}^{n}\left(f(x'_i)-f(x_i)\right),$$
where — number of images, — clear image, — attacked image, — attacked IQA/VQA metric.
Relative gain
$$Rel. gain = \frac{1}{n}\sum_{i=1}^{n}\frac{f(x'_i)-f(x_i)}{f(x_i) + 1},$$
where — number of images, — clear image, — attacked image, — attacked IQA/VQA metric.
Robustness score [17] is defined as the average ratio of maximum allowable change in quality prediction to actual change over all attacked images in a logarithmic scale:
$$R_{score} = \frac{1}{n}\sum_{i=1}^{n}log_{10}( \frac{max\{\beta_1 - f(x'_i), f(x_i) - \beta_2\}}{|f(x'_i)-f(x_i)|} ).$$
As metric values were scaled, we used and .
Next two scores are defined as corresponding distances between distributions multiplied by the sign of the difference between the mean values before and after the attack.
Wasserstein score [18].
$$W_{score} = W_1(\hat{P}, \hat{Q}) \cdot sign(\bar{x}_{\hat{P}} - \bar{x}_{\hat{Q}})$$; $$W_1(\hat{P},\hat{Q}) = \inf_{\gamma \in \Gamma(\hat{P},\hat{Q})} \int_{\mathbb{R}^2} |x-y| d\gamma(x,y) = \int_{-\infty}^{\infty} |\hat{F}_{\hat{P}}(x) - \hat{F}_{\hat{Q}}(x)| dx.$$
Energy Distance score [19].
$$E_{score} = E(\hat{P}, \hat{Q})\cdot sign(\bar{x}_{\hat{P}} - \bar{x}_{\hat{Q}}),$$ $$E(\hat{P},\hat{Q}) = (2 \cdot \int_{-\infty}^{\infty} (\hat{F}_{\hat{P}}(x) - \hat{F}_{\hat{Q}}(x))^2 dx)^{\frac{1}{2}},$$
where and — empirical distributions of metric values before and after the attack, and — their respective empirical Cumulative Distribution Functions, and — their respective sample means.
Large positive values: upward shift of the metric’s predictions.
Values near zero: the absence of the metric’s response to the attack.
Negative values: a decrease in the metric predictions and the inefficiency of the attack.
IQA/VQA metrics calculation
We used public source code for all metrics without additional pretraining and selected the default parameters to avoid overfitting. The training and evaluation of attacks on the metrics were fully automated. For our measurement procedures, we employed the CI/CD tools within a GitLab repository. UAP-based attacks (UAP, cumulative UAP and generative UAP) were used with 3 different amplitudes (0.2, 0.4 and 0.8) and averaged.
Hardware
Calculations were made using the following hardware:
- GeForce RTX 3090 GPU, an Intel(R) Xeon(R) Gold 6226R CPU @ 2.90GHz
- NVIDIA RTX A6000 GPU, AMD EPYC 7532 32-Core Processor @ 2.40GHz
All calculations took a total of about 2000 GPU hours. The values of parameters (, number of iterations, etc.) for the attacks are listed in supplementary material.
References
- NIPS 2017: Adversarial Learning Development Set.
- Ian J. Goodfellow, Jonathon Shlens, and Christian Szegedy. Explaining and harnessing adversarial examples. In 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings, 2015.
- Alexey Kurakin, Ian J Goodfellow, and Samy Bengio. Adversarial examples in the physical world. In Artificial intelligence safety and security, pages 99–112. Chapman and Hall/CRC, 2018.
- Yinpeng Dong, Fangzhou Liao, Tianyu Pang, Hang Su, Jun Zhu, Xiaolin Hu, and Jianguo Li. Boosting adversarial attacks with momentum. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 9185–9193, 2018.
- Qingbing Sang, Hongguo Zhang, Lixiong Liu, Xiaojun Wu, and Alan Bovik. On the generation of adversarial samples for image quality assessment. Available at SSRN 4112969.
- Anish Mittal, Rajiv Soundararajan, and Alan C Bovik. Making a “completely blind” image quality analyzer. IEEE Signal processing letters, 20(3):209–212, 2012.
- Seyed-Mohsen Moosavi-Dezfooli, Alhussein Fawzi, Omar Fawzi, and Pascal Frossard. Universal adversarial perturbations. In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 1765--1773.
- Chaoning Zhang, Philipp Benz, Tooba Imtiaz, and In So Kweon. Understanding adversarial examples from the mutual influence of images and perturbations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 14521–14530.
- Omid Poursaeed, Isay Katsman, Bicheng Gao, and Serge Belongie. Generative adversarial perturbations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 4422--4431.
- Jari Korhonen and Junyong You. Adversarial attacks against blind image quality assessment models. In Proceedings of the 2nd Workshop on Quality of Experience in Visual Multimedia Applications, pages 3–11, 2022.
- Zhou Wang and Eero P Simoncelli. Maximum differentiation (mad) competition: A methodology for comparing computational models of perceptual quantities. Journal of Vision, 8(12):8–8, 2008.
- Tsung-Yi Lin, Michael Maire, Serge Belongie, James Hays, Pietro Perona, Deva Ramanan, Piotr Dollár, and C Lawrence Zitnick. Microsoft coco: Common objects in context. In Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, September 6-12, 2014, Proceedings, Part V 13, pages 740–755. Springer, 2014.
- Mark Everingham, SM Ali Eslami, Luc Van Gool, Christopher KI Williams, John Winn, and Andrew Zisserman. The PASCAL Visual Object Classes Challenge 2012 (VOC2012) Results. http://www.pascal- network.org/challenges/VOC/voc2012/workshop/index.html.
- Tianfan Xue, Baian Chen, Jiajun Wu, Donglai Wei, and William T Freeman. Video enhancement with task-oriented flow. International Journal of Computer Vision (IJCV), 127(8):1106–1125, 2019.
- Derf’s collection.
- Weixia Zhang, Dingquan Li, Xiongkuo Min, Guangtao Zhai, Guodong Guo, Xiaokang Yang, and Kede Ma. Perceptual attacks of no-reference image quality models with human-in-the-loop. arXiv preprint arXiv:2210.00933, 2022.
- Leonid V. Kantorovich. Mathematical methods of organizing and planning production. Management Science, 6(4):366–422, 1960.
- Lev Klebanov. N-Distances and their Applications. 01 2005.
-
MSU Benchmark Collection
- Video Saliency Prediction Benchmark
- LEHA-CVQAD Video Quality Metrics Benchmark
- Learning-Based Image Compression Benchmark
- Super-Resolution for Video Compression Benchmark
- Video Colorization Benchmark
- Defenses for Image Quality Metrics Benchmark
- Super-Resolution Quality Metrics Benchmark
- Deinterlacer Benchmark
- Metrics Robustness Benchmark
- Video Upscalers Benchmark
- Video Deblurring Benchmark
- Video Frame Interpolation Benchmark
- HDR Video Reconstruction Benchmark
- No-Reference Video Quality Metrics Benchmark
- Full-Reference Video Quality Metrics Benchmark
- Video Alignment and Retrieval Benchmark
- Mobile Video Codecs Benchmark
- Video Super-Resolution Benchmark
- Shot Boundary Detection Benchmark
- The VideoMatting Project
- Video Completion
- Codecs Comparisons & Optimization
- VQMT
- MSU Datasets Collection
- Metrics Research
- Video Quality Measurement Tool 3D
- Video Filters
- Other Projects
